Aplicaciones web educativas en R

• 

R Shiny: herramienta en potencia para facilitar el proceso de enseñanza-aprendizaje

¡Hola a todos amigos!

En esta hermosa tarde de noviembre, aprovecharemos para platicarles un poco acerca del lenguaje de programación R y la poderosa librería Shiny, con la cual puedes diseñar tu propia aplicación web interactiva de manera increíblemente sencilla, te invitamos a conocer el poder de R Shiny probando la siguiente app, con la que podrás conocer entre otras cosas, las propiedades de los primeros diez millones de números naturales:

https://atltl.shinyapps.io/niko/

---

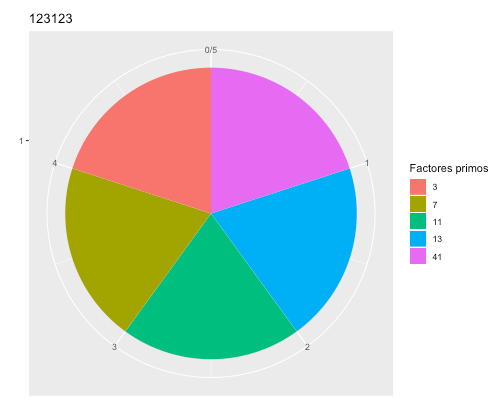
En la imagen de portada (al inicio), se muestra una grafica de pastel con cinco rebanadas, las cuales representan la proporción de los factores primos del numero 123123, los cuales son:
3, 7, 11, 13 y 41.

Si hacemos el producto de los factores primos de un numero, reconstruimos el numero original:

3 x 7 x 11 x 13 x 41 = 123123

---

Nota curiosa:

¿Recuerdan algo así como?

«El orden de los factores no altera el producto»

Esta oración habla específicamente de una multiplicación (producto). Los factores no son mas que los elementos que se multiplican. Pero esto no aplica para cualquier operación. Por ejemplo, en la división. Cuando no hay alteración por el orden de operado, decimos que la operación es conmutativa.

---

La aplicación fue bautizada con el nombre «Nicómaco», en honor al filósofo y matemático Nicómaco de Gerasa (primero en clasificar los números naturales en abundantes, deficientes y perfectos, según la suma de sus divisores propios) te permite conocer tanto los divisores propios de un número como la suma de los mismos. Obtener los factores primos y su clasificación según de Gerasa, entre otras cosas.

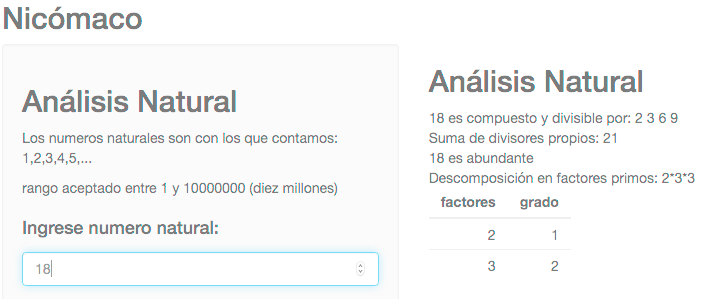
Con Nicómaco, podemos introducir los conceptos de número natural, numero primo y compuesto, de divisores y factores, entre otros, de una manera didáctica, interactiva y divertida. Aprovechando la tecnología que ofrece la amplia paquetería de librerías de R y unas cuantas funciones propias.

Además, Nicómaco contiene un espiral de Ulam interactivo, con el que se puede, una vez comprendidas las definiciones de números primos y compuestos (y saber que no existe una «fórmula» para obtener el n-ésimo primo) sumergirnos en la curiosidad visual del aparente orden en el caos de distribución primal sobre estos fabulosos espirales, donde podrá controlar tanto el número de vueltas cómo el número de entradas.

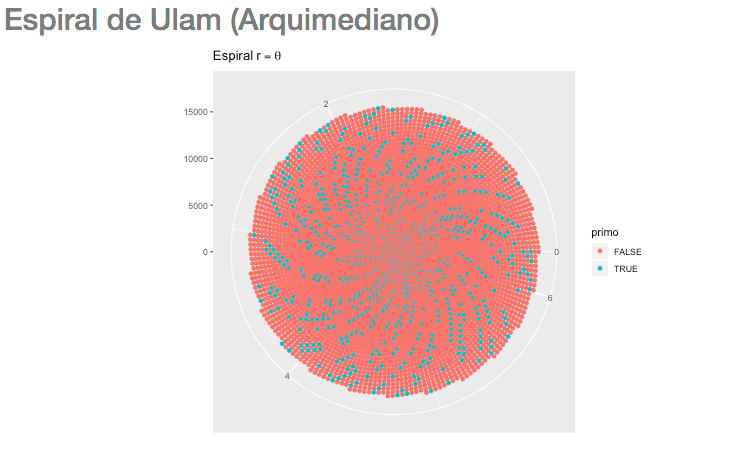
A continuación presentamos una intrigante animación del espiral de Ulam que se obtuvo variando el numero de entradas mientras se mantenía un numero de vueltas constante, con 10 capturas por segundo…

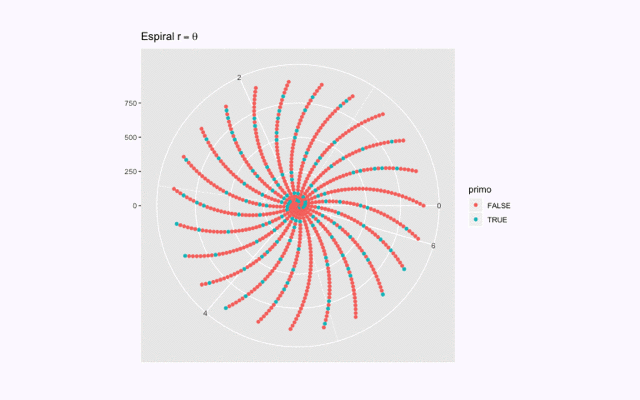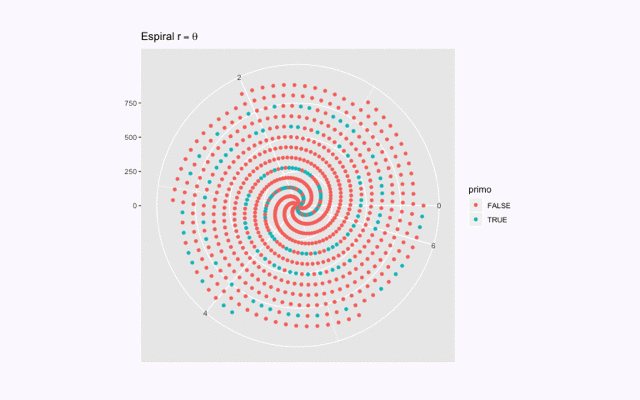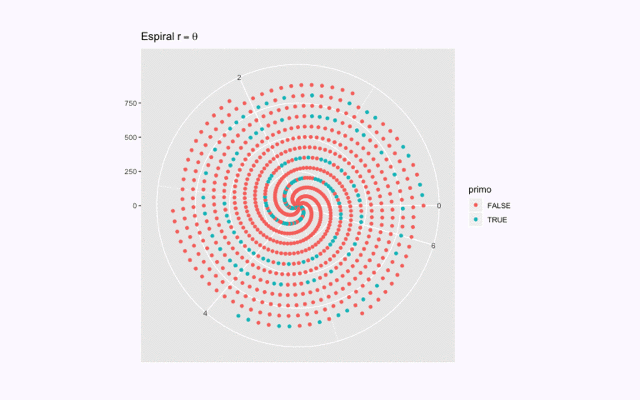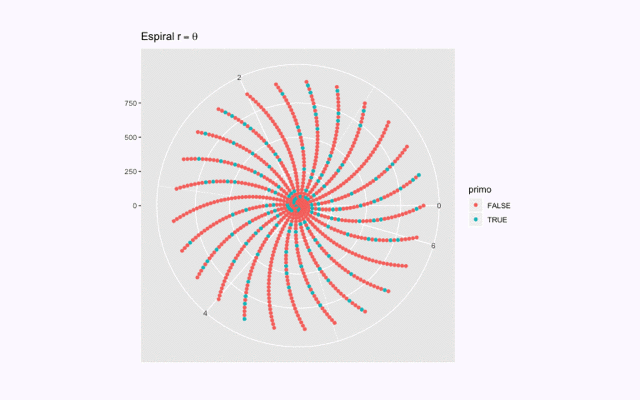
Aquí dejamos el script con las funciones que se utilizaron para generar gifs de este tipo.
A la función create_gif() se le indica intervalo [a,b] y numero de vueltas. Se crean (b-a) imágenes en el directorio de trabajo en el que se encuentre. Con las que puede generar un gif con ayuda de una aplicación como PicGif (OSX).

## Script que genera b-a graficas para creac gif
## Function that plots Ulam Arquimedian Spiral (Pseudo Stach spiral, Stach gives 1 turn por cada cuadrado perfecto)
prime.spiral <- function(obs,vueltas){
  vueltas <- vueltas * 2  
  data.frame(x = seq(0, vueltas * pi, length.out = obs), primo = sapply(1:obs,chkp)) %>% mutate(theta = x %% (2 * pi), r = x) %>%
  ggplot() + aes(x = theta, y = r, colour = primo) +
  coord_polar(start = - pi / 2, direction = - 1) + 
  ggtitle(expression(Espiral~r == theta)) + geom_point() +
  ylim(0, vueltas * pi) + xlim(0, 2 * pi) +
  labs(x = NULL, y = NULL)
}

create_gif <- function(a,b,vueltas){
	v <- a:b
	for(n in v){
		myplot <- prime.spiral(n, vueltas) 
		png(paste("plot", n, ".png", sep = ""))
		print(myplot)
		dev.off()
	}
}

Se recomienda crear una carpeta especial para almacenar los archivos png creados por create_gif() y asignarla como directorio de trabajo. Una vez hecho esto basta con introducir las funciones anteriores y hacer:

create_gif(num_entradas_inicial, num_entradas_final, num_vueltas)

Ejemplo:

create_gif(100, 150, 20)

crea (150-100) = 50 imágenes de un espiral de veinte vueltas. iniciando con 100 entradas y aumentando de una en una hasta 150. Con estas 50 imágenes se puede crear un gif como el mostrado arriba con ayuda de algún software que genere gifs a partir de un conjunto de imágenes, software muy común hoy en día.

¡Espero que les haya parecido interesante y les deseo lo mejor!

–Atl Tlachinolli