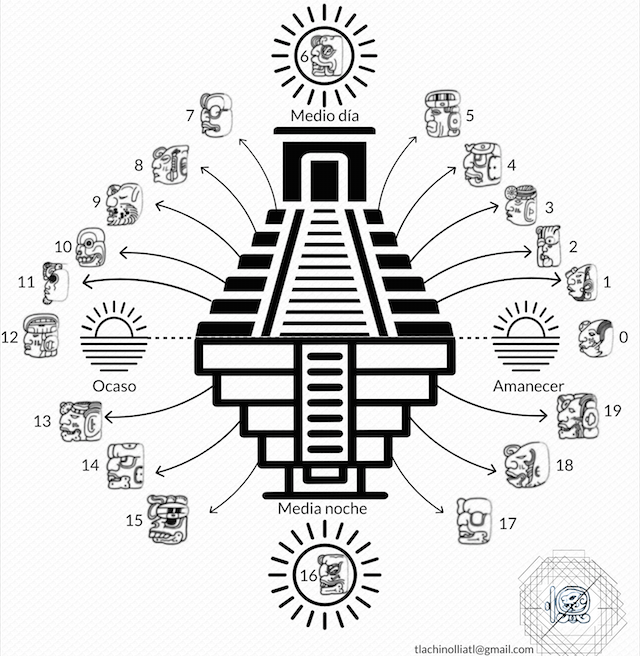
Correspondencia entre numerales cefalomorfos y la cosmología maya.
Cuenta la leyenda maya que los primeros en tener relaciones sexuales fueron el sol y la luna. Al recibir la patada de un venado, ella obtiene una hendidura por la cual el sol realiza la primera penetración (Puente, 2010). A partir de este acto surgen trece dioses. Estos trece dioses están asociados a los primeros numerales mayas en sus «variantes de cabezas». Se menciona que de estos trece, dos de ellos fueron los creadores de los demás (Ibarra, 2018).
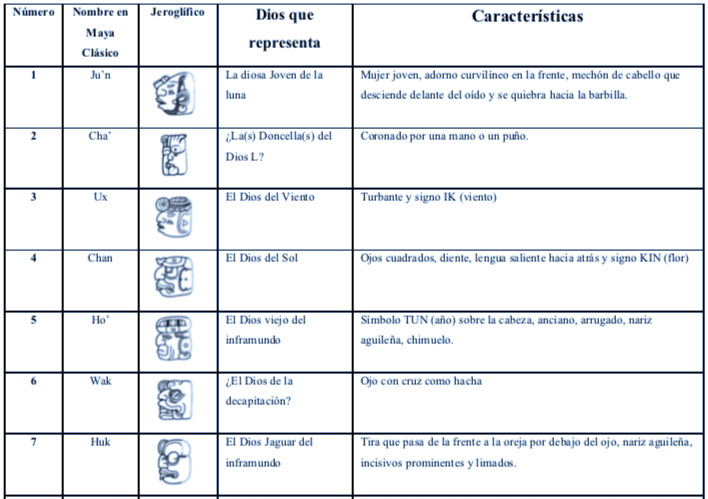
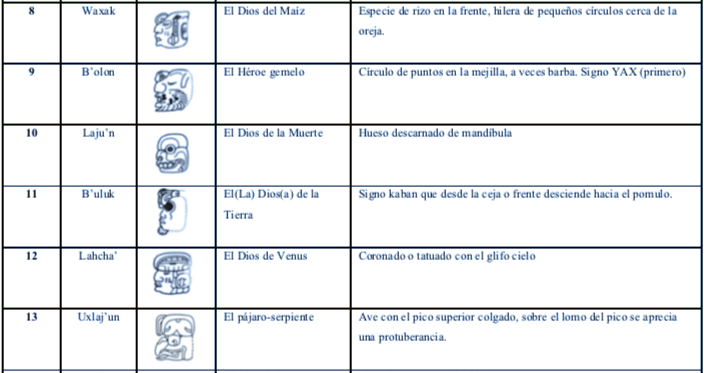
La manera en la que construyen los numerales restantes y así completar los necesarios para su sistema vigesimal –se requieren de veinte símbolos en un sistema vigesimal– , parece aludir al paso de estos primeros dioses por el inframundo. Al componerse tomando las características de los numerales del 14-19 y las del dios de la muerte. Incluso hay una forma alternativa de representar al 13. Además del pájaro-serpiente, el trece se puede formar utilizando los atributos del jeroglífico del 3 y el 10, dios de la muerte. De esta manera el sistema es consistente con los nombres de los numerales en maya clásico, en donde hay 12 nombres distintos para 1-12 y para 13-19 se utilizan los mismos nombres de 3-9, agregándoles la terminación laju’n, correspondiente a 10. En diversas lenguas mayenses laj se puede traducir como «final» (Puente, 2010).

Es interesante que los primeros dos dioses –o números– no tienen representación en el mundo de los muertos. Quizás esto señale la importancia de estos primeros dos números-dioses y podría indicar que son los creadores mencionados en la mitología que menciona Ibarra (2018).
El cero representaba tanto el vacío como lo completo o finalizado. Tanto el inicio cómo el fin (Blume, 2011).

Trece es un número de suma importancia en la cosmovisión maya, hace referencia a los trece niveles del cielo. Los niveles corresponden a trece posiciones que toma el sol durante su travesía celeste, paso que forma la figura de una pirámide de base cuadrada –característica de las culturas de Anáhuac – cada nivel tiene un dios protector (El devenir en el mundo subterráneo, s. f.).
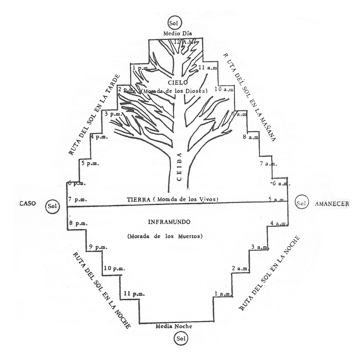
Para los mayas, la tierra es un plano que se extiende en cuatro direcciones. Se encuentra entre el cielo y las aguas del inframundo. Es representado mediante una tortuga sobre la cual crece un árbol sagrado –ceiba o maíz– extendiendo sus ramas hacia el cielo y sus raíces hacia las profundidades del reino de los muertos (El devenir en el mundo subterráneo, s. f.).
En la parte inferior, existen otros nueve niveles por los que el sol pasaba durante la noche, niveles considerados del inframundo (El devenir en el mundo subterráneo, s. f.).

Existe una correspondencia entre los primeros trece numerales mayas, sus dioses y sus trece niveles del cielo. Parecen insinuarse algunas correspondencias en los numerales restantes y los nueve niveles del inframundo. Se hace alegoría a la muerte o final para componer los numerales 13-19 que llamaremos «compuestos», como si los mismos dioses del cielo estuvieran en su paso por el inframundo recordándonos que «como es arriba es abajo».
Considerando que los mayas tenían un día cero para cada mes en su calendario solar –aunque en realidad no es un cero sino el final de un mes y al mismo tiempo el inicio de otro– y que este representa tanto inicio como fin (Blume, 2011). Parece sobria la idea de que este deba tener un lugar tanto en la morada de los vivos como en la de los muertos. Por otro lado el numeral del 12 es el punto medio entre los dioses del cielo y del inframundo –es también final e inicio–, por lo que se podría decir lo mismo respecto a pertenecer a los dos mundos.
Siguiendo este modelo, parece que todo se acomoda de manera natural. Los siete dioses muertos quedan en el inframundo. El dios en la posición mas alta del cielo, es el mismo que el de la posición mas baja en el mundo de los muertos –en su representación de inframundo–. Tanto en los numerales correspondientes con los niveles del cielo como con los del inframundo, este dios divide los grupos de manera equitativa.
En el grupo de los vivos, se encuentra entre seis numerales menores y seis mayores.
En el grupo de los muertos, se encuentra entre cuatro menores y cuatro mayores.

De esta forma tenemos 13 niveles en la parte superior –reino de los cielos–, representados por los dioses 0-12, y 9 niveles en la parte inferior –reino de los muertos– representados por los dioses 12-0 –este último cero se puede pensar al cero como final, como un ciclo completo– acomodando a todas las representaciones «muertas» en el inframundo. Los dioses 0 y 12 actúan de manera dual, mediadores de mundos.
Referencias
Blume, A. (2011). Maya Concepts of Zero. Proceedings of the American Philosophical Society, 155(1), 51-88
El devenir en el mundo subterráneo. (s. f.). Recuperado 4 de febrero de 2021, de http://www.revista.unam.mx/vol.13/num11/art108/?fbclid=IwAR01VMHxuTQ-l-cXQUKnniOf45yI0_DHBEShGGnY7ijwersTMMgiUUkJzck
Ibarra, L. (2018). The Mayan Gods: An Explanation from the Structures of Thought. Journal of Historical Archaeology & Anthropological Sciences, 3. https://doi.org/10.15406/jhaas.2018.03.00071
Kettunen, H., & Helmke, C. (s. f.). 11th European Maya Conference Malmö, December 4th–9th, 2006. 121.
Maya Number System & Math. (2019, octubre 17). Planet Archaeology. https://planetarchaeology.co.uk/maya-number-system/
Puente, F. B. (2010). Tsik: Los números y la numerología entre los mayas. Instituto Nacional de Antropología e Historia.


