Cultivando información de la web

«Manitas de buda»
[Fotografía de Miguel Andrade]. (Rancho Viejo, Veracruz. 2019).

Minando artistas amigos

Antes que nada le doy las gracias a mi compañera de vida y mejor amiga Ladrón de Mar, quien me asistió en la grabación del video siguiendo la actividad generando dudas y aclaraciones.

Preámbulo

Que tal queridas personas. Espero que se encuentren llenas de salud y amor en estos tiempos de cambio. Esta entrada del blog fue inspirada por el canal de facebook Coronatv (@CoronaTV2020) y particularmente por una lectura realizada por Hunaac-cel: Músico, rapero y distinguido miembro del grupo. La lectura fue acerca de “La dictadura de los datos: La verdadera historia desde dentro de Cambridge Analytica y cómo el Big Data, Trump y Facebook corrompieron la democracia, y cómo puede volver a pasar”, libro de Brittany Kaiser, y nos platicó un poco acerca de cómo se crean perfiles psicológicos a partir de la información que dejamos tirada como basura en redes sociales (sí, likes y toda esa mierda). Resulta escalofriante la exactitud con la que pueden conocernos una vez que tienen suficientes datos, como recomendación podemos dar «Me gusta» y «Seguir» a cosas que no nos gustan para que no tengan un perfil tan preciso. Hacer esto también ayuda a que la información que se te presente (noticias, anuncios, etc.) no esté sesgada al tema definido de forma algorítmica como «de tu agrado».

Al finalizar esta actividad habremos aprendido:

Algo de programación
Raspar información de la web
codificar y ejecutar un script

Introducción

Hoy platicaremos un poco acerca de cómo extraer información de la red, utilizaremos el lenguaje de programación R. Este lenguaje de programación tiene un enfoque al análisis estadístico y ha evolucionado tanto que ya puedes hacer casi cualquier cosa con su ayuda. Los invito a visitar este par de páginas web que construímos con R.

Coronavirus (Web app para ver tasa de infectados/muertos que raspa información diariamente de OMS)

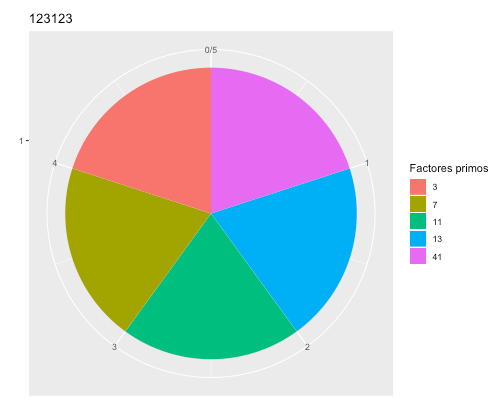
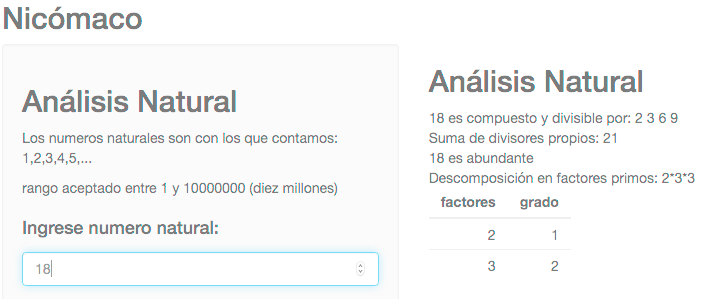
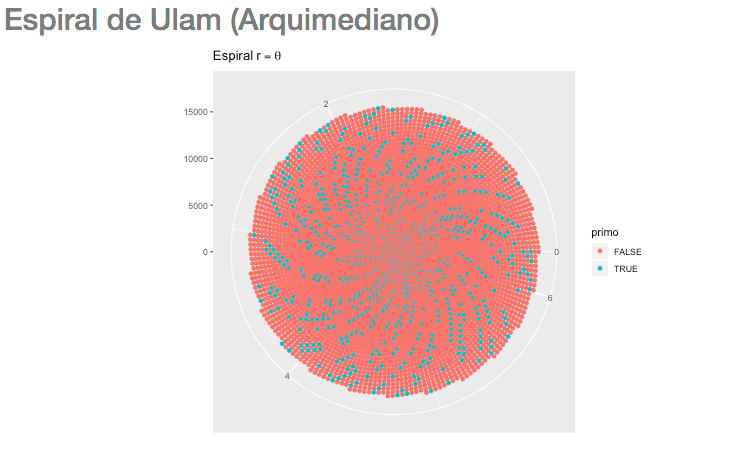
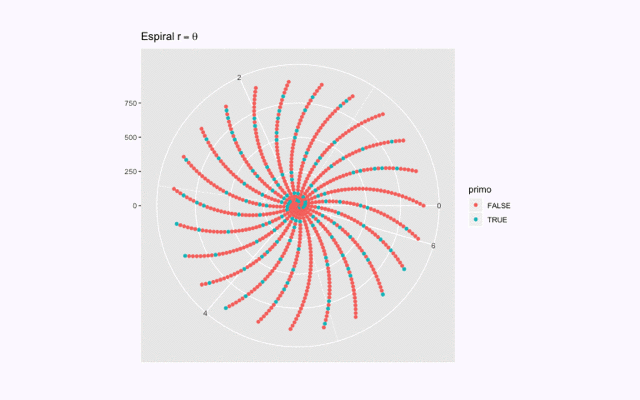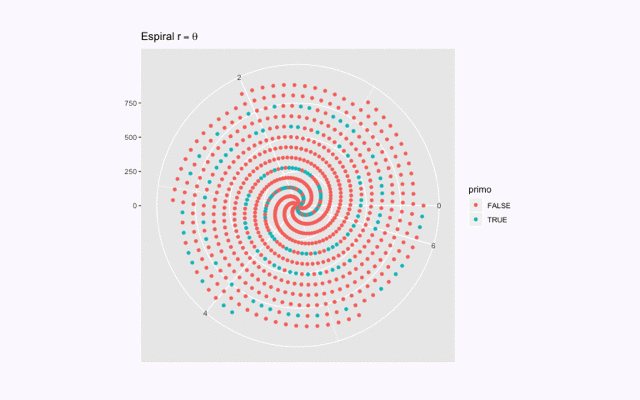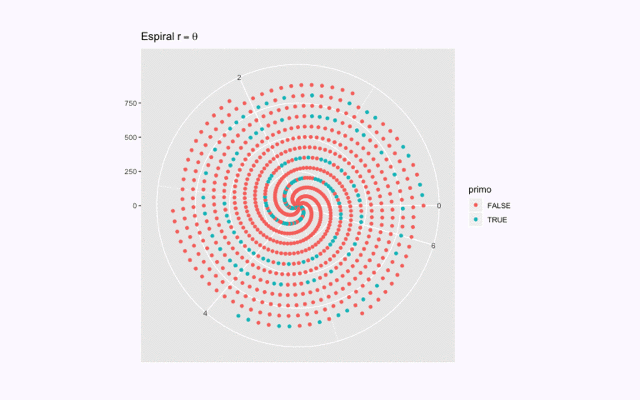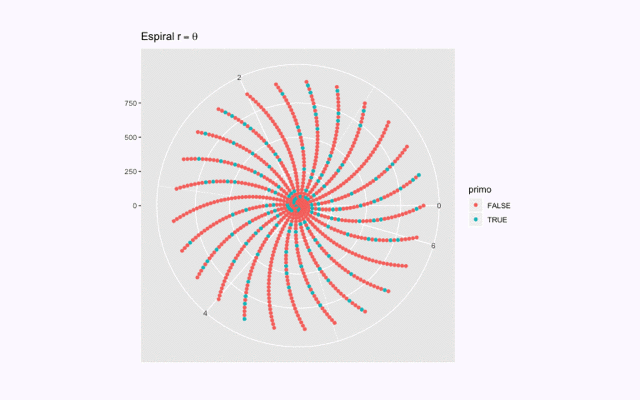
Nicómaco (Web app para analizas números naturales y jugar con espirales de números primos)

Instalación

Si no tienes R puedes descargarlo aquí:

para Windows:

https://cran.r-project.org/bin/windows/base/

para Mac:

https://cran.r-project.org/bin/macosx/

instale R y prosiga con la actividad.

Resumen

Comenzaremos con un ejercicio sencillo obteniendo información de la URL

http://www.discogs.com

El cual es una base de datos de la música. Pero, la idea al fondo de esta actividad, es sembrar los conocimientos básicos para que cada quien pueda hacer sus propios proyectos de cultivo de datos.

En esta actividad, construiremos un script (archivo con serie de líneas de código que realiza una tarea específica al ser ejecutado) que al ejecutarlo nos pida el nombre de una artista y el programa automáticamente entre a la página del artista en discogs y extraiga la información de artistas que han colaborado con el artista buscado. A continuación agrego una captura de una ejecución del script en donde género la lista de «artistas amigos» o «colaboradores» de el artista buscado: Lassi Nikko.

La actividad es sencilla y se realiza paso a paso de manera que pueda seguirse sin mucho esfuerzo y esta destinada a cualquier público, sin importar si tiene o no conocimientos de programación. El video se realiza junto con un asistente que nos apoyará con generar dudas y preguntas durante la actividad de manera que sirva de ayuda a cualquiera que llegue a frenar su avance en la actividad debido a confusión o mal interpretación.

Actividad

Video de actividad, síguenos en Youtube.

Si eres de los que prefiere leer, aquí puedes consultar la actividad desarrollada en forma textual, que también puede servir como material de apoyo para resolver alguna duda del video.

http://www.mediafire.com/file/8wt0u9bsnhc3658/Mining_artist_friends.html/file

Dicho esto, no dejen de escribir con sus dudas, comentarios, sugerencias, correcciones. Las cuales leo y contesto con mucho gusto.

Me despido con los mejores deseos para todos ustedes.

– Atl Tlachinolli

Afina tu Arduino con una escala igualmente temperada eligiendo tu propia entonación

¡Liberate del La a 440 Hz!

¡Hola a todos amigos!

Espero encontrarlos muy bien en este caluroso mes de marzo.

He aquí un Arduino muy barroco al que le encanta tararear Bach. Lo interesante de este Arduino es que es capaz de afinar la escala a partir de un La medio ingresado por el usuario, con ayuda de la función tuneScale() se genera una escala igualmente temperada de 12 notas como output a partir de dicho «la» medio, recibido como input.

Para este sketch, basta cambiar el valor de la4 en la línea de código número 12.

De esta manera nuestro Arduino rompió la jaula de la entonación en «La 440 Hz» a la que se le había querido encasillar en una precoz etapa del bosquejo.

La motivación para escribir este código fue escuchar las diferencias de afinación en escalas igualmente temperadas al elegir un La medio en el intervalo [400,450]Hz como «guía de afinación». Pues, se sabe que la afinación con un la de 440 Hz, no fue normalizada sino hasta 1995 con ISO 16, antes del cual se consideraba aceptable cualquier «la» del intervalo [400,450]Hz, siendo un La de alrededor de 430 Hz el predominante en muchas escuelas.

Función para afinar escala a partir de La medio ingresado (A4)

La curiosidad de escuchar una misma melodía con variaciones en la afinación de la escala igualmente temperada, fue motivación suficiente para escribir el siguiente bosquejo con el cual puedes elegir el valor de tu la medio o «guía de afinación» para después apreciar un fragmento del hermoso preludio No.1 en do mayor, parte del clavecín bien temperado, escrito por el maestro Bach.

A continuación se comparte el bosquejo de Arduino para su propio deleite:

////////////////////////////////////////////////////////////////////////////////////////////////////////////
//  Tune me & I Play you Bach – Arduino Bach player with user defined tuning – tlachinolliatl@gmai.com /////
//  Visit our life Blog at:                                                                            /////   
//                         http://www.atl.travel.blog                                                         ///// 
////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// The inspiration behind this code was to hear the differences in equal temperament tuning  varying the value of the key note A4   ////
// standardly tuned at 440 Hz with some controversy about better harmonic generation with 432 cicles per second (Hz).               ////
//  Overall, there was a tendency towards the end of the 18th century for the frequency of the A above middle C to be in the range  ////
// of 400 to about 450 Hz.                                                                                                          ////  
////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// change following value for tuning the scale
double la4 = 400; // checar como puede modificar este valor el usuario durante ejecución
//recomendación: definir los tiempos, h de half: d, w, h, q
int h=250; // aquí solo se definió h, ya que para esta melodía no habrá variación de tiempo en las notas.
// cent function recieves number of cents n and returns proportion factor to use it in tuneScale function to create user tuned scale
double centFactor(int n){
    double proportion;
    double power;
    power = (double)n/12; // por no hacer el casting todo valía nepe
    proportion = pow(2, power);
    return proportion;
  }
// The Tune function
double * tuneScale(double la4){
    static double  scale[12]; // arreglo para guardar las notas generadas
    // a partir de middleA podemos obtener Do de una octava mas arriba, que es la que utilizaremos
    // por medio de la siguiente formula de Cents, introducida por Alexander Ellis en 1875
    // b = a*2^(n/1200) 
    // se obtiene cualquier nota b por medio de la nota a y el numero n de cents en el intervalo de a hasta b
    double do5;
    do5 = la4*centFactor(3);
    for (int i = 0; i < 12; i++) {
      scale[i] = do5*centFactor(i);
   }
  return scale;
  }
double * scale = tuneScale(la4); // creation of the scale from tuneScale function and predefined la4
double  C = scale[0], //definimos las frecuencias de las notas
        Cs = scale[1],
        D = scale[2],
        Ds = scale[3],
        E = scale[4],
        F = scale[5],
        Fs = scale[6],
        G = scale[7],   
        Gs = scale[8],
        A = scale[9],
        As = scale[10],
        B = scale[11], 
        PAU = 30000; //pausa

int random_tonal_row, random_note = 0;        
// array of 15 tonal rows consisting of 16 notes each
double melody[15][16] = { // consider array as [number of melody rows][number of notes on each melody row]

  // The Well-Tempered Clavier, BWV 846: Prelude No. 1 in C major (Fragment)

                   { C/2, E/2, G/2, C, E, G/2, C, E, C/2, E/2, G/2, C, E, G/2, C, E },
                   
                   { C/2, D/2, A/2, D, F,  A/2, D, F, C/2, D/2, A/2, D, F,  A/2, D, F },
                   
                   { B/4, D/2, G/2, D, F, G/2, D, F, B/4, D/2, G/2, D, F, G/2, D, F },
                   
                   { C/2, E/2, G/2, C, E, G/2, C, E, C/2, E/2, G/2, C, E, G/2, C, E} ,

                   { C/2 , E/2 , A/2 , E, A, A/2, E, A, C/2 , E/2 , A/2 , E, A, A/2, E, A },

                   { C/2, D/2, Fs/2, A/2, D, Fs/2, A/2, D, C/2, D/2, Fs/2, A/2, D, Fs/2, A/2, D },

                   { B/4, D/2, G/2, D, G, G/2, B/2, G, B/4, D/2, G/2, D, G, G/2, B/2, G },

                   { B/4, C/2, E/2, G/2, C, E/2, G/2, C, B/4, C/2, E/2, G/2, C, E/2, G/2, C },

                   { A/4, C/2, E/2, G/2, C, E/2, G/2, C, A/4, C/2, E/2, G/2, C, E/2, G/2, C },

                   { Fs/4, A/4, D/2, A/2, C, D/2, A/2, C, Fs/4, A/4, D/2, A/2, C, D/2, A/2, C },

                   { G/4, B/4, D/2, G/2, B/2, D/2, G/2, B/2, G/4, B/4, D/2, G/2, B/2, D/2, G/2, B/2 },

                   { G/4, As/4, E/2, G/2, Cs, E/2, G/2, Cs, G/4, As/4, E/2, G/2, Cs, E/2, G/2, Cs },
                     
                   { F/4, A/4, D/2, A/2, D, D/2, A/2, D, F/4, A/4, D/2, A/2, D, D/2, A/2, D }, 

                   { F/4, D/2, F/2, Gs/2, B/2, F/2, Gs/2, B/2, F/4, D/2, F/2, Gs/2, B/2, F/2, Gs/2, B/2 },

                   { E/4, C/2, E/2, G/2, C, E/2, G/2, C, E/4, C/2, E/2, G/2, C, E/2, G/2, C }
                   
                   };

void setup() {
  // put your setup code here, to run once:
  pinMode(11, OUTPUT); // fija pin 11 como salida
  Serial.begin(9600); //for freakin' printin'
}

void loop() {
  for (int i = 0; i < 15; i++) {  
    //random_tonal_row = random(0,15); // definimos renglon tonal de manera aleatoria. Para random(min,max) el mínimo es inclusivo mientras el maximo es exlcusivo
    Serial.println();
     // imprimimos en serial para rescatar posibles combincaciones interesantes al utilizar random
    //Serial.print(":");
      for(int j = 0 ; j < 16; j++){
        Serial.print(melody[i][j]);
        //random_note = random(0,17); // 17 no existe es para agregar posible pausa
        //Serial.print(random_note);
        Serial.print("\t"); // tabulador para distinguir renglones tonales de mas de dos digitos
        tone(11, melody[i][j]); //da el tono a la frecuencia de la nota del ciclo, le pasamos el renglon tonal aleatorio para las 16 notas o podemos pasarle también random note.
        delay(h);//se mantiene con la nota el tiempo definido, para tiempos mas complejos se puede hacer un arreglo similar a melody
        noTone(11); //finaliza la nota
      }
  }
  //Serial.println();
}

El código anterior pueden descargarlo en el enlace compartido a continuación:

¡Haz clic aquí para descargar Arduino_i_play_u_bach sketch!

Cualquier pregunta, duda, aclaración o recomendación acerca del código por favor háganla saber escribiendo un correo en la sección de contacto.

Aquí pueden escuchar un par de grabaciones de audio con fines demostrativos donde se compara la apreciación de un fragmento de BWV 846: Prelude No. 1 in C major ejecutado con una escala igualmente temparada en la entonación normalizada con A4 = 440 Hz seguida de una entonación de 400 Hz. ¿Cual te parece mas armónica?

Escuchar BWV 846 afinado en base a «la» medio de 400Hz

Escuchar BWV 846 afinado en base a «la» medio de 440Hz

Ejercicios propuestos:

Modifica el código para que la melodía sea reproducida al revés.
Modifica el código para que se reproduzcan los renglones tonales de forma aleatoria.
Modifica el código para que reproduzca las notas de la melodía de forma aleatoria.

¡Saludos y feliz primavera!

Aplicaciones web educativas en R

Proporción de factores primos del numero 123123

R Shiny: herramienta en potencia para facilitar el proceso de enseñanza-aprendizaje

¡Hola a todos amigos!

En esta hermosa tarde de noviembre, aprovecharemos para platicarles un poco acerca del lenguaje de programación R y la poderosa librería Shiny, con la cual puedes diseñar tu propia aplicación web interactiva de manera increíblemente sencilla, te invitamos a conocer el poder de R Shiny probando la siguiente app, con la que podrás conocer entre otras cosas, las propiedades de los primeros diez millones de números naturales:

https://atltl.shinyapps.io/niko/

En la imagen de portada (al inicio), se muestra una grafica de pastel con cinco rebanadas, las cuales representan la proporción de los factores primos del numero 123123, los cuales son:
3, 7, 11, 13 y 41.

Si hacemos el producto de los factores primos de un numero, reconstruimos el numero original:

3 x 7 x 11 x 13 x 41 = 123123

Nota curiosa:

¿Recuerdan algo así como?

«El orden de los factores no altera el producto»

Esta oración habla específicamente de una multiplicación (producto). Los factores no son mas que los elementos que se multiplican. Pero esto no aplica para cualquier operación. Por ejemplo, en la división. Cuando no hay alteración por el orden de operado, decimos que la operación es conmutativa.

La aplicación fue bautizada con el nombre «Nicómaco», en honor al filósofo y matemático Nicómaco de Gerasa (primero en clasificar los números naturales en abundantes, deficientes y perfectos, según la suma de sus divisores propios) te permite conocer tanto los divisores propios de un número como la suma de los mismos. Obtener los factores primos y su clasificación según de Gerasa, entre otras cosas.

Con Nicómaco, podemos introducir los conceptos de número natural, numero primo y compuesto, de divisores y factores, entre otros, de una manera didáctica, interactiva y divertida. Aprovechando la tecnología que ofrece la amplia paquetería de librerías de R y unas cuantas funciones propias.

Además, Nicómaco contiene un espiral de Ulam interactivo, con el que se puede, una vez comprendidas las definiciones de números primos y compuestos (y saber que no existe una «fórmula» para obtener el n-ésimo primo) sumergirnos en la curiosidad visual del aparente orden en el caos de distribución primal sobre estos fabulosos espirales, donde podrá controlar tanto el número de vueltas cómo el número de entradas.

Espiral con 7107 entradas, 2470 vueltas.

A continuación presentamos una intrigante animación del espiral de Ulam que se obtuvo variando el numero de entradas mientras se mantenía un numero de vueltas constante, con 10 capturas por segundo…

Aquí dejamos el script con las funciones que se utilizaron para generar gifs de este tipo.
A la función create_gif() se le indica intervalo [a,b] y numero de vueltas. Se crean (b-a) imágenes en el directorio de trabajo en el que se encuentre. Con las que puede generar un gif con ayuda de una aplicación como PicGif (OSX).

## Script que genera b-a graficas para creac gif
## Function that plots Ulam Arquimedian Spiral (Pseudo Stach spiral, Stach gives 1 turn por cada cuadrado perfecto)
prime.spiral <- function(obs,vueltas){
  vueltas <- vueltas * 2  
  data.frame(x = seq(0, vueltas * pi, length.out = obs), primo = sapply(1:obs,chkp)) %>% mutate(theta = x %% (2 * pi), r = x) %>%
  ggplot() + aes(x = theta, y = r, colour = primo) +
  coord_polar(start = - pi / 2, direction = - 1) + 
  ggtitle(expression(Espiral~r == theta)) + geom_point() +
  ylim(0, vueltas * pi) + xlim(0, 2 * pi) +
  labs(x = NULL, y = NULL)
}

create_gif <- function(a,b,vueltas){
	v <- a:b
	for(n in v){
		myplot <- prime.spiral(n, vueltas) 
		png(paste("plot", n, ".png", sep = ""))
		print(myplot)
		dev.off()
	}
}

Se recomienda crear una carpeta especial para almacenar los archivos png creados por create_gif() y asignarla como directorio de trabajo. Una vez hecho esto basta con introducir las funciones anteriores y hacer:

create_gif(num_entradas_inicial, num_entradas_final, num_vueltas)

Ejemplo:

create_gif(100, 150, 20)

crea (150-100) = 50 imágenes de un espiral de veinte vueltas. iniciando con 100 entradas y aumentando de una en una hasta 150. Con estas 50 imágenes se puede crear un gif como el mostrado arriba con ayuda de algún software que genere gifs a partir de un conjunto de imágenes, software muy común hoy en día.

¡Espero que les haya parecido interesante y les deseo lo mejor!

–Atl Tlachinolli

Como acelerar tu código de R

Fi de Euler en la mirilla — –Toc toc… –¿Quién es? –Fi de Euler…

Deja de escribir «R a la C» y aprovecha la verdadera velocidad de R

¡Mira este video si no estas de humor para leer!

Resumen

Para escribir código veloz en R tomamos en cuenta tres cosas:

Pruebas lógicas
Subconjuntos
Ejecuciones simultaneas de elementos de un objeto

El código que las utilice en lugar de ciclos for con condiciones if será por lo general más rápido.

Esto pasa por que R, a diferencia de lenguajes como C, no compila antes de ejecutar. Durante la compilación, la computadora optimiza el uso de la memoria para los ciclos for, es por eso que corren rápido en C, pero en R, debemos hacer uso de las Pruebas lógicas, Subconjuntos y Ejecuciones simultaneas de elementos para sacar provecho de sus características y así obtener el mayor beneficio (la mayoría de las veces).

Se optimizaron las funciones del paquete R Qurra, obteniendo una mejora notoria en tiempo de ejecución, mediante el uso de estos tres principios. También se obtienen los primeros 1000 valores de la función Fi de Euler en tan solo veinte segundos (en un equipo del 2009).

Introducción

En la entrada anterior compartimos un pequeño paquete de funciones de R, resultado de un ejercicio de iniciación realizado después de repasar la sintaxis y conceptos fundamentales. Aunque las funciones cumplieron su cometido, estábamos cayendo en una mala costumbre típica de programadores que se mudan de lenguajes cómo C a R.

G. Grolemund, autor de Hands-On R Programming, libro excelente que comparto a continuación:

https://rstudio-education.github.io/hopr/

diría que estábamos «hablando R con acento de C»…

Es decir, utilizando un montón de ciclos for con condiciones if dentro (sin tomar en cuenta que R no compila) en lugar de aprovechar las características que hacen a R tan poderoso, en una palabra, la vectorización. Se re-escribió el código del paquetito de funciones pero ahora sí, «a la R», e hicimos luchar las distintas versiones de funciones chkprime para verificar que se haya conseguido una mejora en tiempo de ejecución.

Procedimiento

Se escribió una segunda versión del paquete de funciones R Qurra, la cual se comparte a continuación:

rqurra2.0.R

intentando evitar ciclos for con condiciones if dentro y se trató de implementar todo mediante pruebas lógicas, subconjuntos y ejecución simultánea de elementos.

Se escribió la función fight para hacer competir a la familia de funciones chkprime, tomando el tiempo que demoran en hallar los primos en los intervalos:

[1,1000] , [1,10000] y [1,100000]

y observar las mejoras en tiempo de ejecución.

La función regresa un data frame listo para utilizarse para graficar en ggplot (paquete de R).

se escribió la función phi que recibe n natural como argumento y regresa phi(n) donde phi es la función Fi de Euler, función de suma importancia en teoría de números y el sistema de cifrado RSA.

Resultados

En este video se muestra como correr el script y utilizar las funciones, así como resultados y conclusiones:

Gráfica de comparación de velocidad de familia de funciones chkprime* (realizada con ggplot2 y data frame que regresa la función fight), observe que a pesar de que el tiempo de ejecución de la familia es muy similar para una longitud de 1000 (punto de partida), a medida que seguimos avanzando observamos que la función chkprime «a la C» (en rojo) se empieza a quedar atrás y es rebasada incluso por la chkprime.r (en verde) que está muy poco optimizada (por no decir otra cosa).

Comparación de tiempo de ejecución entre familia de funciones que encuentran primos — Comparación de velocidad de la familia de funciones chkprime

Con ayuda de la función testrlpr reloaded, la cual revisa si un par de números son primos relativos entre si, se diseñó la función phi, que regresa el valor de la función Fi de Euler, es decir, le pasas un natural como argumento y te regresa la cantidad o cardinalidad del conjunto de primos relativos de ese número que sean menores que el mismo. Se obtuvieron los primeros diez mil valores de la función para realizar la gráfica siguiente.

Gráfica de primeros 10000 valores de función Fi de Euler, creada con ggplot.
(obtenidos en aprox. 110 minutos con la función phi en cpu Intel i5 2.4Ghz con 4 GB de RAM)

Gráfica de primeros 10000 valores de la función fi de Euler — La función fi se relaciona con el sistema de cifrado RSA, el cual ocupa primos enormes para el encriptado

Conclusiones

A pesar de todo, no hay que pensar que es malo usar ciclos for en R, pero recordar este par de consejos podría ser útil:

Si observas un ciclo for con un if dentro, lo mas seguro es que puedas remplazarlo con operaciones de subconjuntos y condiciones lógicas y este será mas veloz.
Si es necesario utilizar un ciclo for, trata de minimizar su bloque de código para que se realice lo menos posible dentro del mismo.

En R la mayoría de las funciones están vectorizadas, por lo que al aplicarlas a un vector se hace a todos los elementos del vector al mismo tiempo, evitando demoras, mientras un loop for lo haría uno por uno (y sin el boost que le daría la compilación), esta es la causa por la cual es preferible evitarlos de ser posible, en la mayoría de los casos.

Una parte muy importante de la programación en cualquier lenguaje es la reutilización de código. En la ciencia de datos, es prudente aprovechar también cualquier información ya existente antes de generarla uno mismo, así se logra completar proyectos en menor tiempo. Por ejemplo, seguro en algún lugar en la red podemos encontrar los primeros diez mil (o más) valores de la función Fi de Euler. Nosotros hubieramos podido ahorrar los 110 minutos que se tardó la función phi en hallar los primeros diez mil valores que utilizamos para la gráfica. También pudimos haber utilizado alguna función para checar primos disponible en la red en lugar de perder tiempo escribiendo las nuestras… Pero la idea de escribir estos pequeños paquetes de funciones, es que nos sirva de ejercicio para: acostumbrarnos a la sintaxis de R, entender el manejo de las estructuras de control que ofrece R para después poder comprender, modificar y unir cualquier código que hallemos y que el tiempo que perdimos en escribir estos «paquetitos de funciones» se recupere a la hora de solucionar las tareas de código del futuro. Lo que queremos decir es; si todavía no te sientes como un experto de R, es mejor que escribas unas cuantas funciones por ti mismo antes de querer reutilizar código ya existente. Así cómo crear algunos vectores, matrices, listas y marcos de datos para acostumbrarse a su manejo y filtrado.

¡Los mejores deseos para todos ustedes!

– Atl Tlachinolli

Programación en R

Los primeros cuatro primos se encuentran entre el uno y el diez. Si los sumas, el resultado es 17

Números: primos, primos relativos perfectos y amigos

Aprendiendo R con curiosidades matemáticas

Preámbulo

¿Qué tal Tlachinollis?

En lo personal, por acá se podría decir que somos mas adeptos de ANSI C pero debemos comentar que nos estamos enamorando de R. Este poderoso, intuitivo y eficaz lenguaje, te permite aprender a programar evitando conceptos complicados como declaración de variables, apuntadores y asignación de memoria, es la herramienta perfecta para el estudiante de ciencias e ingenierías o para cualquiera con una curiosidad inherente por los números.

Confesaremos ser novatos en R, lo poquito que hemos escrito son unas funciones muy sencillas para el manejo de tablas generadas por sistemas de rastreo deportivo ZXY (ZXY Sport tracking systems), las cuales pueden hallarse aquí:

R ZXY Sport Tracking data edition tools

esto ya fue hace tres años y a hachazos, sin saber mucho de R se fue implementando en unos tres días por que así fue el plazo de trabajo, hicimos lo que se pidió… pero digamos que sin aprender de forma adecuada, o al menos como hubiésemos deseado en caso de haber tenido mas tiempo.

Ahora estamos desempolvando o más bien re-aprendiendo con paciencia y con ayuda de un par de libros excelentes para iniciarse, los cuales se encuentran en la red en varios sitios, aquí les dejo la lista con los enlaces por si les interesa:

La mejor manera de aprender es con las manos a la obra. Después de refrescarnos un poco de la sintaxis de R para quitarnos el chip ANSI C, algunos resultados fueron las siguientes funciones que sirven para revisar curiosidades matemáticas como números primos, números perfectos, números amigos y primos relativos, que son funciones muy básicas que presentan un buen ejercicio para el aprendizaje de un nuevo lenguaje de programación, además pueden llegar a ser de utilidad para estudiantes de cursos cómo fundamentos de álgebra . En fin, quisimos compartirlas, esperamos que a alguien le sean útiles.

Código

A continuación se muestra el código fuente y explicaremos como pueden usarse las funciones para pasar un buen rato.

¡Hágalo usted mismo!

Tan solo copie y pegue el siguiente código en la consola de R y presione introducir, con lo que estará listo para jugar con las funciones :

# R Qurra packet
# functions to test primes, relative primes, perfect and friend numbers
# This package may be useful for undergraduate students in Fundaments of Algebra courses
# where you are usually introduced deeply into this concepts and their properties
# tlachinolliatl@gmail.com
#########################################################################

# Function that checks for primality
# returns TRUE in case n prime, FALSE instead
# try checking primality for first 100 natural numbers like this:
# > chkrprime(1:100)
chkprime <- function(x){
	primo <- vector()
	j <- 1
	for(n in x){
		primo[j] <- T
		for(i in 2:(sqrt(n))){
			if(n%%i==0 && n!=2){
				primo[j] <-F
				break
			}
		}
	j <- j+1		
	}
return(primo)
}
# Function that returns a list of proper divisors of a given set of numbers
# divp stands for (div)isores (p)ropios
#
divp <- function (x){
	k <- 1
	lista <- list()
	for(n in x){
		divisores <- vector()
		j <- 1	
		for(i in 2:(n/2)){
			if(chkprime(n)) break # not looping if n is prime
			if(n%%i==0){
				divisores[j] <-i
				j <- j+1
			}
		}
	lista[[k]] <- c(1,divisores)
	k <- k + 1			
	}
return(lista)
}

# Function that checks if a pair of numbers are friends between them
# if friends, testfrnd returns TRUE, else it will return FALSE
#
#  Muhammad Baqir Yazdi found the pair (9363584,9437056) in the XVII century 
# Checking this pair took a couple of minutes for my old Intel Core 2 Duo at 2.13 GHz
# Try with  (1184, 1210) for faster computation
testfrnd <- function(x,y){
	divpx <- unlist(divp(x)) # is the same divp(x)[[1]]?
	divpy <- unlist(divp(y))
	sumx <- sum(divpx)
	sumy <- sum(divpy)
	if(sumx==y && sumy==x){
		return(T)
	}else return(F)
}
#Function that checks if two numbers x,y are relative primes between them
# i.e. MCD(x,y) = 1 i.e. they have no common proper divisors between them !=1
# if relative primes, testrprime returns TRUE, else it will return FALSE
testrlpr <- function(x,y){
	divpx <- unlist(divp(x))
	divpy <- unlist(divp(y))
	if(length(divpx)==1 && divpx[1]==1 || length(divpy)==1 && divpy[1]==1){
		return(T)
	}else
	if(any(divpx[2:length(divpx)]==divpy[2:length(divpy)])){
		return(F)
	}else return(T)
}

#Function that checks if a number is perfect
# i.e the sum of his proper divisors (including one) add up to the same number
# Example: proper divisors of 6 are 1, 2, 3 wich sum 1+2+3 = 6 the number itself
# RETURNS TRUE IF NUMBER IS PERFECT FALSE INSTEAD 
# Find the perfectos between 1:10000 with a crazy R loop like this:
# > for(i in 1:10000) if(testprfc(i)) print(i)
# be patient it may take a while
testprfc <- function(x){
	divpx <- unlist(divp(x))
	sumx <- sum(divpx)
	if(sumx==x){
		return(T)
	}else return(F)
}

En el siguiente video se muestra como sacarle un poco de jugo a estas funciones desde la consola de R, lo cual puede ser una práctica para cualquiera que se esté iniciando en este lenguaje:

Si tienes comentarios para mejorar el código o algún consejo de R relacionado con las funciones anteriores será muy apreciado.

¡Nos despedimos con los mejores deseos!

De los números he aprendido:

«Si quieres llegar a ser perfecto comienza por ser tu propio amigo»

– E.P. del Cerro