numeros primos – Atl Tlachinolli

Fi de Euler en la mirilla — –Toc toc… –¿Quién es? –Fi de Euler…

Deja de escribir «R a la C» y aprovecha la verdadera velocidad de R

¡Mira este video si no estas de humor para leer!

Resumen

Para escribir código veloz en R tomamos en cuenta tres cosas:

Pruebas lógicas
Subconjuntos
Ejecuciones simultaneas de elementos de un objeto

El código que las utilice en lugar de ciclos for con condiciones if será por lo general más rápido.

Esto pasa por que R, a diferencia de lenguajes como C, no compila antes de ejecutar. Durante la compilación, la computadora optimiza el uso de la memoria para los ciclos for, es por eso que corren rápido en C, pero en R, debemos hacer uso de las Pruebas lógicas, Subconjuntos y Ejecuciones simultaneas de elementos para sacar provecho de sus características y así obtener el mayor beneficio (la mayoría de las veces).

Se optimizaron las funciones del paquete R Qurra, obteniendo una mejora notoria en tiempo de ejecución, mediante el uso de estos tres principios. También se obtienen los primeros 1000 valores de la función Fi de Euler en tan solo veinte segundos (en un equipo del 2009).

Introducción

En la entrada anterior compartimos un pequeño paquete de funciones de R, resultado de un ejercicio de iniciación realizado después de repasar la sintaxis y conceptos fundamentales. Aunque las funciones cumplieron su cometido, estábamos cayendo en una mala costumbre típica de programadores que se mudan de lenguajes cómo C a R.

G. Grolemund, autor de Hands-On R Programming, libro excelente que comparto a continuación:

https://rstudio-education.github.io/hopr/

diría que estábamos «hablando R con acento de C»…

Es decir, utilizando un montón de ciclos for con condiciones if dentro (sin tomar en cuenta que R no compila) en lugar de aprovechar las características que hacen a R tan poderoso, en una palabra, la vectorización. Se re-escribió el código del paquetito de funciones pero ahora sí, «a la R», e hicimos luchar las distintas versiones de funciones chkprime para verificar que se haya conseguido una mejora en tiempo de ejecución.

Procedimiento

Se escribió una segunda versión del paquete de funciones R Qurra, la cual se comparte a continuación:

rqurra2.0.R

intentando evitar ciclos for con condiciones if dentro y se trató de implementar todo mediante pruebas lógicas, subconjuntos y ejecución simultánea de elementos.

Se escribió la función fight para hacer competir a la familia de funciones chkprime, tomando el tiempo que demoran en hallar los primos en los intervalos:

[1,1000] , [1,10000] y [1,100000]

y observar las mejoras en tiempo de ejecución.

La función regresa un data frame listo para utilizarse para graficar en ggplot (paquete de R).

se escribió la función phi que recibe n natural como argumento y regresa phi(n) donde phi es la función Fi de Euler, función de suma importancia en teoría de números y el sistema de cifrado RSA.

Resultados

En este video se muestra como correr el script y utilizar las funciones, así como resultados y conclusiones:

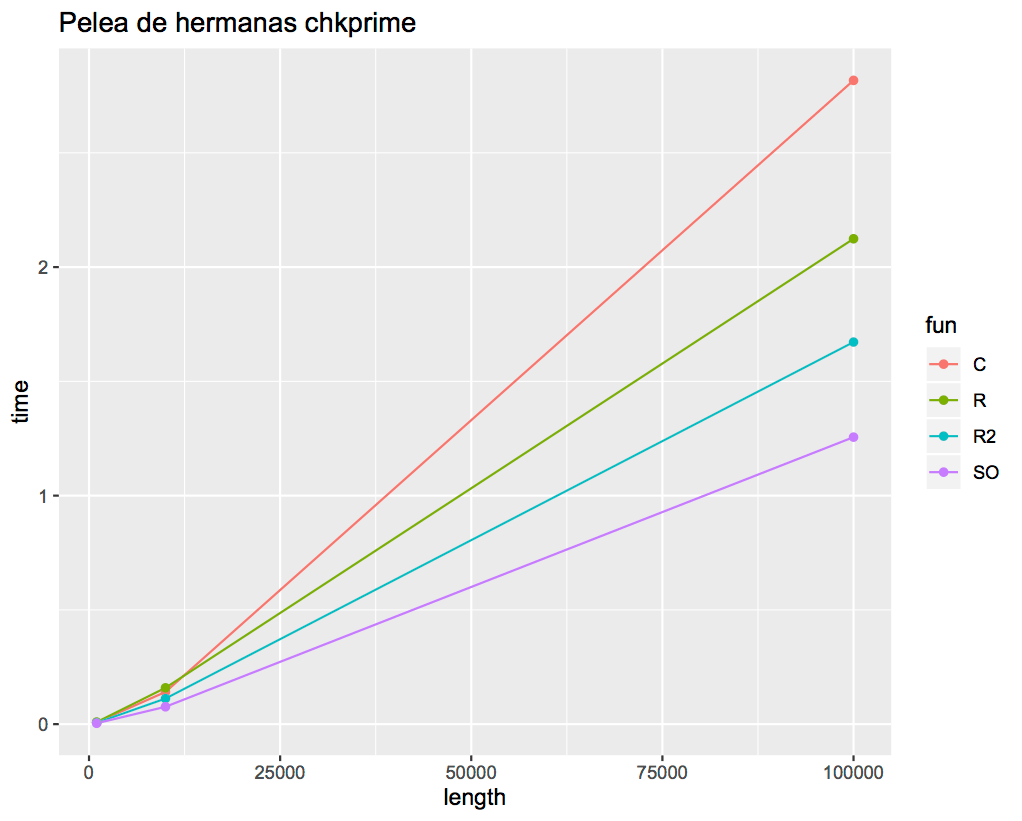
Gráfica de comparación de velocidad de familia de funciones chkprime* (realizada con ggplot2 y data frame que regresa la función fight), observe que a pesar de que el tiempo de ejecución de la familia es muy similar para una longitud de 1000 (punto de partida), a medida que seguimos avanzando observamos que la función chkprime «a la C» (en rojo) se empieza a quedar atrás y es rebasada incluso por la chkprime.r (en verde) que está muy poco optimizada (por no decir otra cosa).

Comparación de tiempo de ejecución entre familia de funciones que encuentran primos — Comparación de velocidad de la familia de funciones chkprime

Con ayuda de la función testrlpr reloaded, la cual revisa si un par de números son primos relativos entre si, se diseñó la función phi, que regresa el valor de la función Fi de Euler, es decir, le pasas un natural como argumento y te regresa la cantidad o cardinalidad del conjunto de primos relativos de ese número que sean menores que el mismo. Se obtuvieron los primeros diez mil valores de la función para realizar la gráfica siguiente.

Gráfica de primeros 10000 valores de función Fi de Euler, creada con ggplot.
(obtenidos en aprox. 110 minutos con la función phi en cpu Intel i5 2.4Ghz con 4 GB de RAM)

Gráfica de primeros 10000 valores de la función fi de Euler — La función fi se relaciona con el sistema de cifrado RSA, el cual ocupa primos enormes para el encriptado

Conclusiones

A pesar de todo, no hay que pensar que es malo usar ciclos for en R, pero recordar este par de consejos podría ser útil:

Si observas un ciclo for con un if dentro, lo mas seguro es que puedas remplazarlo con operaciones de subconjuntos y condiciones lógicas y este será mas veloz.
Si es necesario utilizar un ciclo for, trata de minimizar su bloque de código para que se realice lo menos posible dentro del mismo.

En R la mayoría de las funciones están vectorizadas, por lo que al aplicarlas a un vector se hace a todos los elementos del vector al mismo tiempo, evitando demoras, mientras un loop for lo haría uno por uno (y sin el boost que le daría la compilación), esta es la causa por la cual es preferible evitarlos de ser posible, en la mayoría de los casos.

Una parte muy importante de la programación en cualquier lenguaje es la reutilización de código. En la ciencia de datos, es prudente aprovechar también cualquier información ya existente antes de generarla uno mismo, así se logra completar proyectos en menor tiempo. Por ejemplo, seguro en algún lugar en la red podemos encontrar los primeros diez mil (o más) valores de la función Fi de Euler. Nosotros hubieramos podido ahorrar los 110 minutos que se tardó la función phi en hallar los primeros diez mil valores que utilizamos para la gráfica. También pudimos haber utilizado alguna función para checar primos disponible en la red en lugar de perder tiempo escribiendo las nuestras… Pero la idea de escribir estos pequeños paquetes de funciones, es que nos sirva de ejercicio para: acostumbrarnos a la sintaxis de R, entender el manejo de las estructuras de control que ofrece R para después poder comprender, modificar y unir cualquier código que hallemos y que el tiempo que perdimos en escribir estos «paquetitos de funciones» se recupere a la hora de solucionar las tareas de código del futuro. Lo que queremos decir es; si todavía no te sientes como un experto de R, es mejor que escribas unas cuantas funciones por ti mismo antes de querer reutilizar código ya existente. Así cómo crear algunos vectores, matrices, listas y marcos de datos para acostumbrarse a su manejo y filtrado.

¡Los mejores deseos para todos ustedes!

– Atl Tlachinolli

Los primeros cuatro primos se encuentran entre el uno y el diez. Si los sumas, el resultado es 17

Números: primos, primos relativos perfectos y amigos

Aprendiendo R con curiosidades matemáticas

Preámbulo

¿Qué tal Tlachinollis?

En lo personal, por acá se podría decir que somos mas adeptos de ANSI C pero debemos comentar que nos estamos enamorando de R. Este poderoso, intuitivo y eficaz lenguaje, te permite aprender a programar evitando conceptos complicados como declaración de variables, apuntadores y asignación de memoria, es la herramienta perfecta para el estudiante de ciencias e ingenierías o para cualquiera con una curiosidad inherente por los números.

Confesaremos ser novatos en R, lo poquito que hemos escrito son unas funciones muy sencillas para el manejo de tablas generadas por sistemas de rastreo deportivo ZXY (ZXY Sport tracking systems), las cuales pueden hallarse aquí:

R ZXY Sport Tracking data edition tools

esto ya fue hace tres años y a hachazos, sin saber mucho de R se fue implementando en unos tres días por que así fue el plazo de trabajo, hicimos lo que se pidió… pero digamos que sin aprender de forma adecuada, o al menos como hubiésemos deseado en caso de haber tenido mas tiempo.

Ahora estamos desempolvando o más bien re-aprendiendo con paciencia y con ayuda de un par de libros excelentes para iniciarse, los cuales se encuentran en la red en varios sitios, aquí les dejo la lista con los enlaces por si les interesa:

La mejor manera de aprender es con las manos a la obra. Después de refrescarnos un poco de la sintaxis de R para quitarnos el chip ANSI C, algunos resultados fueron las siguientes funciones que sirven para revisar curiosidades matemáticas como números primos, números perfectos, números amigos y primos relativos, que son funciones muy básicas que presentan un buen ejercicio para el aprendizaje de un nuevo lenguaje de programación, además pueden llegar a ser de utilidad para estudiantes de cursos cómo fundamentos de álgebra . En fin, quisimos compartirlas, esperamos que a alguien le sean útiles.

Código

A continuación se muestra el código fuente y explicaremos como pueden usarse las funciones para pasar un buen rato.

¡Hágalo usted mismo!

Tan solo copie y pegue el siguiente código en la consola de R y presione introducir, con lo que estará listo para jugar con las funciones :

# R Qurra packet
# functions to test primes, relative primes, perfect and friend numbers
# This package may be useful for undergraduate students in Fundaments of Algebra courses
# where you are usually introduced deeply into this concepts and their properties
# tlachinolliatl@gmail.com
#########################################################################

# Function that checks for primality
# returns TRUE in case n prime, FALSE instead
# try checking primality for first 100 natural numbers like this:
# > chkrprime(1:100)
chkprime <- function(x){
	primo <- vector()
	j <- 1
	for(n in x){
		primo[j] <- T
		for(i in 2:(sqrt(n))){
			if(n%%i==0 && n!=2){
				primo[j] <-F
				break
			}
		}
	j <- j+1		
	}
return(primo)
}
# Function that returns a list of proper divisors of a given set of numbers
# divp stands for (div)isores (p)ropios
#
divp <- function (x){
	k <- 1
	lista <- list()
	for(n in x){
		divisores <- vector()
		j <- 1	
		for(i in 2:(n/2)){
			if(chkprime(n)) break # not looping if n is prime
			if(n%%i==0){
				divisores[j] <-i
				j <- j+1
			}
		}
	lista[[k]] <- c(1,divisores)
	k <- k + 1			
	}
return(lista)
}

# Function that checks if a pair of numbers are friends between them
# if friends, testfrnd returns TRUE, else it will return FALSE
#
#  Muhammad Baqir Yazdi found the pair (9363584,9437056) in the XVII century 
# Checking this pair took a couple of minutes for my old Intel Core 2 Duo at 2.13 GHz
# Try with  (1184, 1210) for faster computation
testfrnd <- function(x,y){
	divpx <- unlist(divp(x)) # is the same divp(x)[[1]]?
	divpy <- unlist(divp(y))
	sumx <- sum(divpx)
	sumy <- sum(divpy)
	if(sumx==y && sumy==x){
		return(T)
	}else return(F)
}
#Function that checks if two numbers x,y are relative primes between them
# i.e. MCD(x,y) = 1 i.e. they have no common proper divisors between them !=1
# if relative primes, testrprime returns TRUE, else it will return FALSE
testrlpr <- function(x,y){
	divpx <- unlist(divp(x))
	divpy <- unlist(divp(y))
	if(length(divpx)==1 && divpx[1]==1 || length(divpy)==1 && divpy[1]==1){
		return(T)
	}else
	if(any(divpx[2:length(divpx)]==divpy[2:length(divpy)])){
		return(F)
	}else return(T)
}

#Function that checks if a number is perfect
# i.e the sum of his proper divisors (including one) add up to the same number
# Example: proper divisors of 6 are 1, 2, 3 wich sum 1+2+3 = 6 the number itself
# RETURNS TRUE IF NUMBER IS PERFECT FALSE INSTEAD 
# Find the perfectos between 1:10000 with a crazy R loop like this:
# > for(i in 1:10000) if(testprfc(i)) print(i)
# be patient it may take a while
testprfc <- function(x){
	divpx <- unlist(divp(x))
	sumx <- sum(divpx)
	if(sumx==x){
		return(T)
	}else return(F)
}

En el siguiente video se muestra como sacarle un poco de jugo a estas funciones desde la consola de R, lo cual puede ser una práctica para cualquiera que se esté iniciando en este lenguaje:

Si tienes comentarios para mejorar el código o algún consejo de R relacionado con las funciones anteriores será muy apreciado.

¡Nos despedimos con los mejores deseos!

De los números he aprendido:

«Si quieres llegar a ser perfecto comienza por ser tu propio amigo»

– E.P. del Cerro

Etiqueta: numeros primos

Como acelerar tu código de R